Object Orientation Estimation Algorithm for Visual Feedback Systems

May 7, 2020

Introduction

Let’s try to demonstrate a simple statistical approach to find the orientation of the object. There are already existing complex solutions [4] [5] which draw a significant amount of CPU resources, making it impractical to implement in real-time systems. Especially for moving systems, a delay in the orientation could cost a large deviation(error) from the reference. One of the closest approaches is discussed by Dulio Furtado and Fulton T. Ray, Jr [1].

Now, let’s try to determine the orientation of the object by considering vector “a”(on the principal axis of the object) and x-axis and orientation will be determined by the relative angle between the two. Vector “a” is considered to be the shortest side of the triangle. The triangle will be formed by system generated points. These points can be generated by two methods, if it depends on the shape of the object then Vector-Cosine Polygonal Approximation (VCPA) is used and vertex of the object will be considered or else centroids of internal features of the image will be used by Centroid-Vertex Polygon Formation(CVPF). The limitations of this method are that it’s not applicable for highly symmetrical objects and has forced internal features on the object. While the advantage is that it is unidirectional and hence gives the orientation for 360°. While this method uses VCPA and CVPF and both of these methods are iterative methods.

In proposed method the points are identified using median and quartiles which offers a non-iterative approach.

PROPOSED METHOD

The method is divided into three stages.

Feature Detection

It’s a crucial phase which determines the boundary region of the feature [3] to be considered for identifying the points. These points will then be considered for forming a line segment along the principal axis of the object. The relative angle between the line segment and one of the axes will determine the orientation of the object. The feature to be detected is not governed by the very shape of the feature although it will have effects on the noise. Objects with rotational symmetry of order 4 will restrict to 90°orientation rather than objects with rotational symmetry of order 2 which will give 180°orientation.

Identification of points

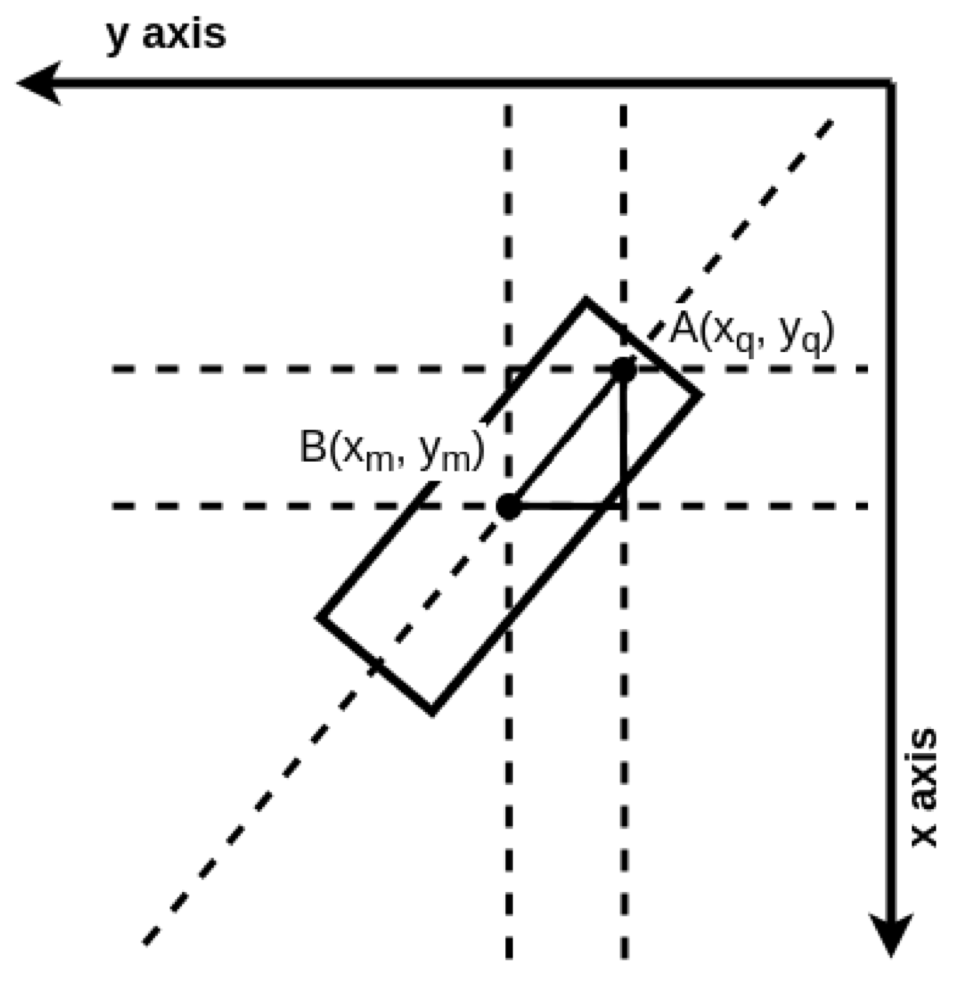
The median and quartiles as shown in “Fig. 1” makes the orientation independent of the shape and position of the feature in the camera frame as median serves as the middle value of the sorted set and quartile being a second point in the feature gives the slope relative to the camera frame. This statistical approach ensures that points will always lie in the boundary values of the feature. Hence a significant amount of error and noise is being avoided and has a robust response.

Determining orientation

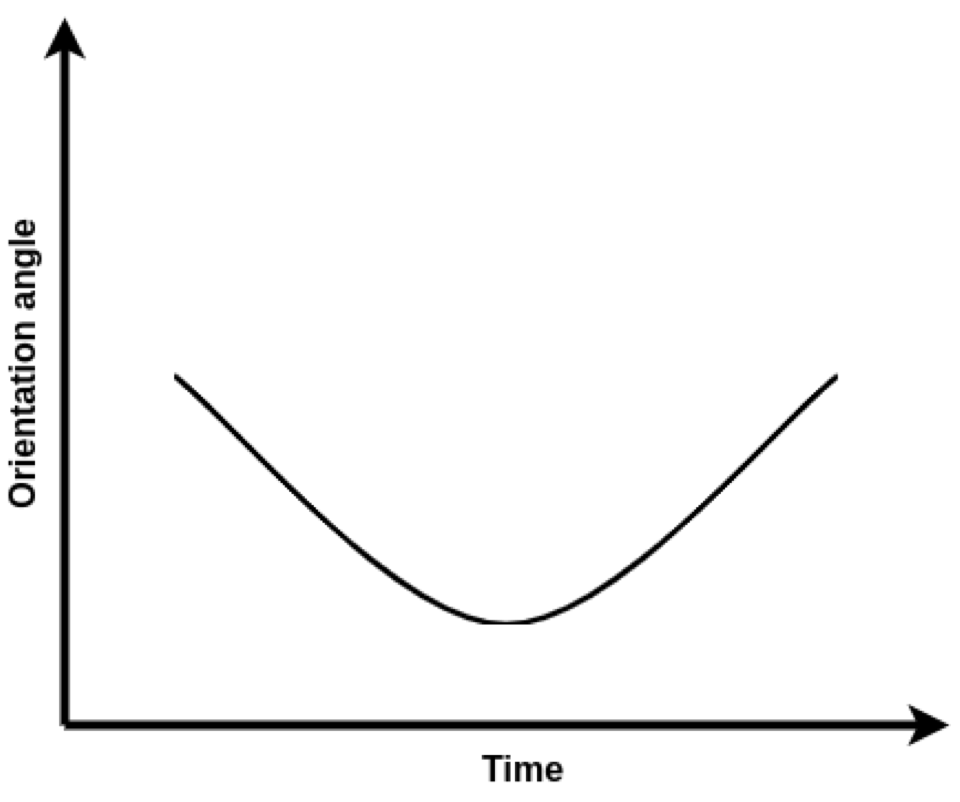
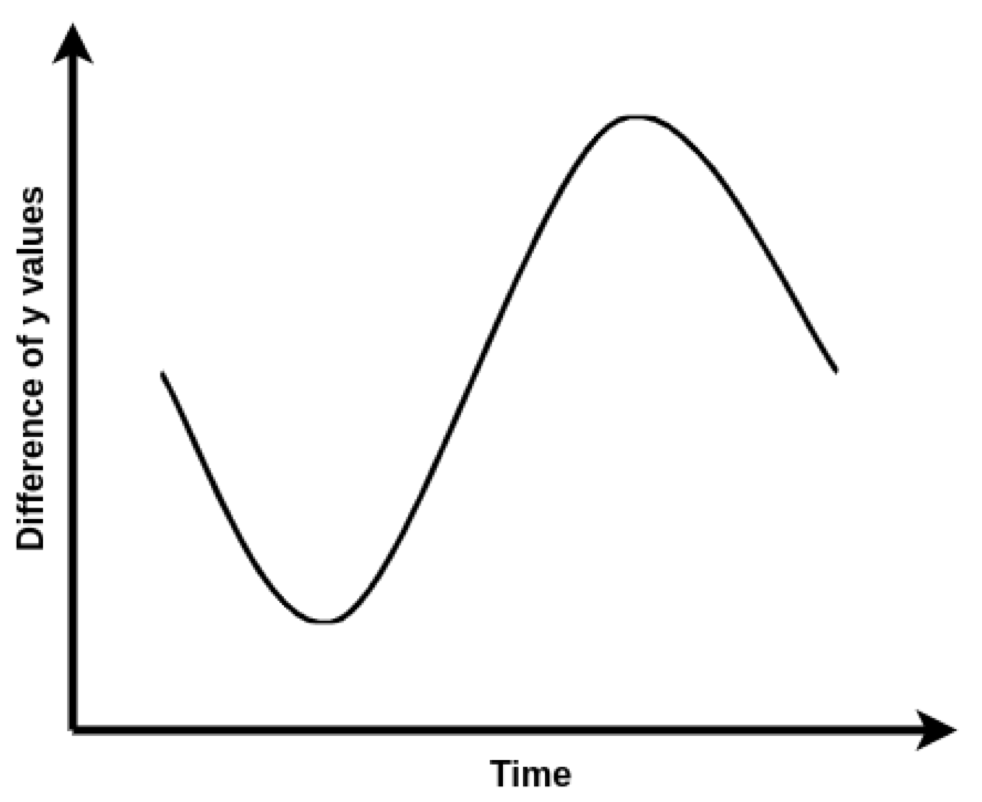
After points have been identified, orientation can easily be calculated by $tan^-1 ( \frac{x}{y} )$. The magnitude of the angle will be calculated by the slope as shown in “Fig. 2” where as the direction(anticlockwise or clockwise)(shown in “Fig. 4”) will be given by the difference of y value respect to index value of x quartile and y median as shown in “Fig. 3”.

IMPLEMENTATION

We tested this on a testbed consisting of a camera [7] [8] fixed orthogonal to the object feature. Feature detection is done based on a unique colour on the object in the camera frame and the feature is a blue rectangular shaped strip. The algorithm is implemented in Python programming language using OpenCV library and been implemented in following steps.

Feature Detection

• Convert the frame into HSV colour model(HSV separates image intensity(environmental parameters) from actual colour code)
• Mask with the required colour code(extraction of the feature based on color).
• Morphological transformation(dilation + erosion) to eliminate the noise.

Identification of points

• Separate row and column of detected feature
• Find row($x_m$) and column($y_m$) median
• Find a quartile with 25% in row($x_q$) and column($y_q$) array from midpoint.
• Find the index of the above value in row array
• For the same index find the value in column index($y_{\text{ind}}$)

Orientation estimation

• Find the slope of the line segment joining $x_m$ , $y_m$ and $x_q$,$y_q$ by $tan^−1(\frac{x_m − x_q }{y_m − y_q})$
• For the direction(anticlockwise or clockwise) will be given by the difference of y value respect to index value of x quartile and y median $y_m − y_{\text{ind}}$

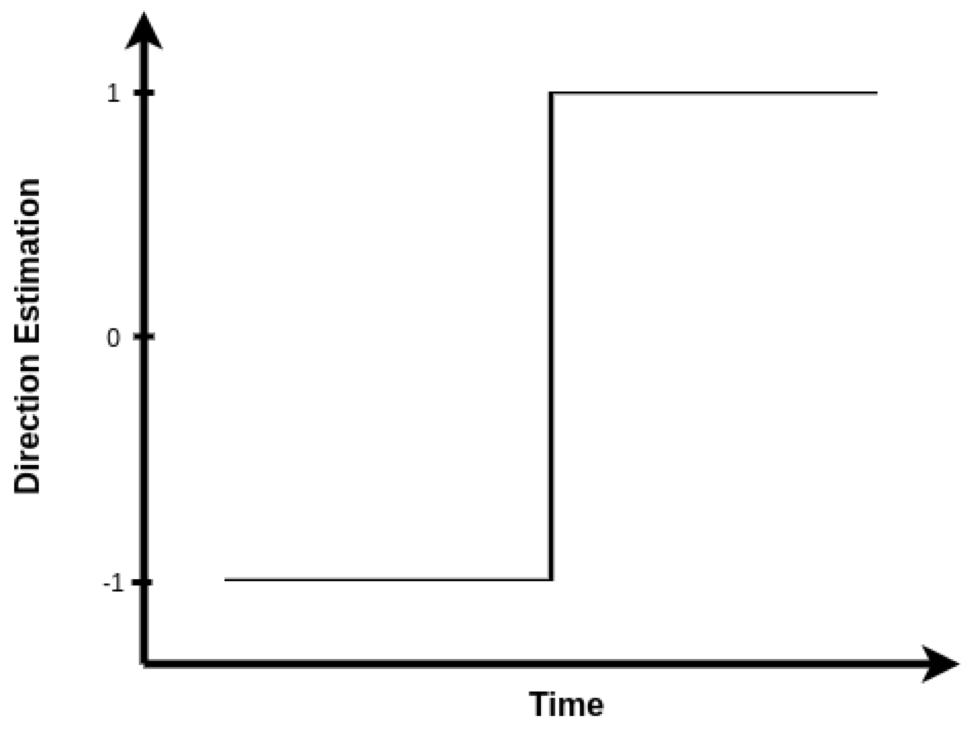
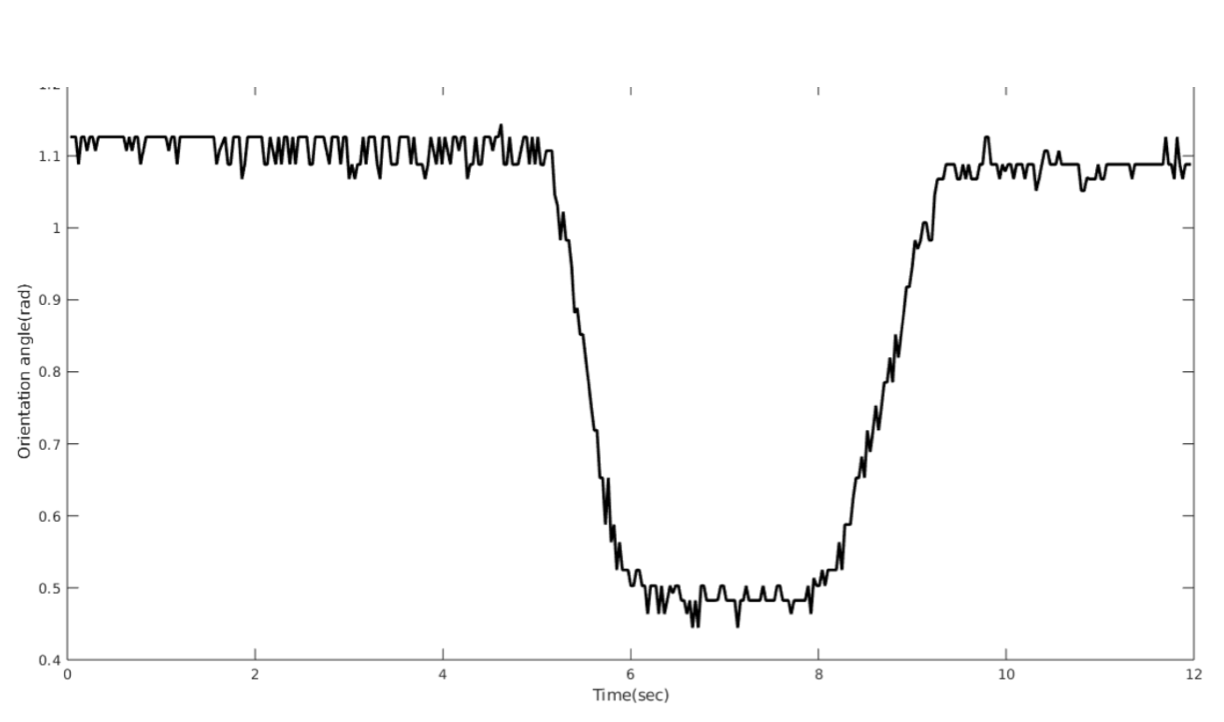
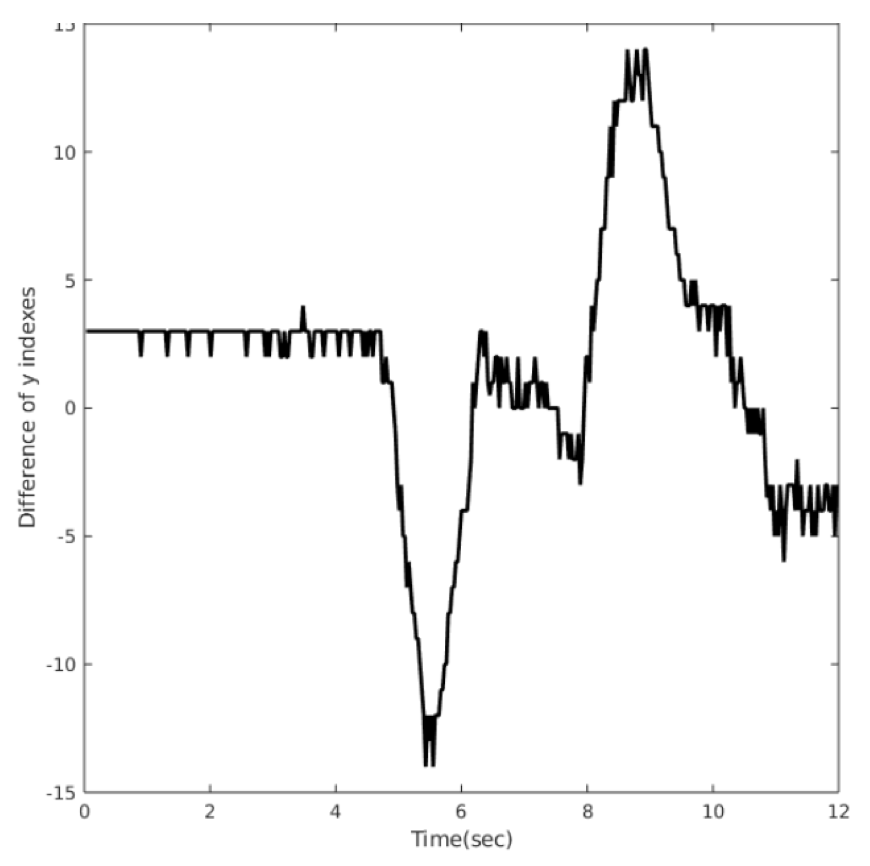
The orientation estimation and direction graphs are shown in “Fig. 5” and “Fig. 8” respectively. The noise due to the difference as shown in “Fig. 6” operation in estimation of direction is filtered with a low pass filter(moving average filter) as shown in “Fig. 7”

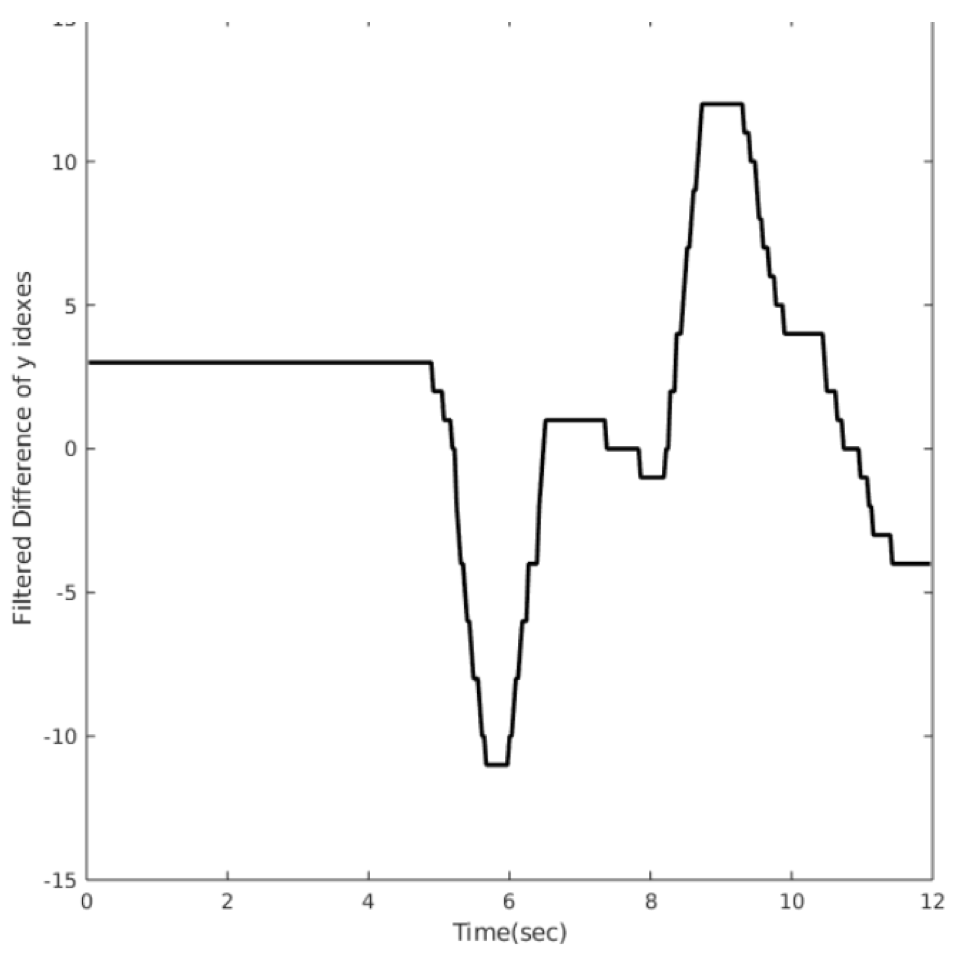
CONCLUSION

Hence a simple statistical method of estimating orientation [6] was implemented for real-time applications. This method is very well applicable to images as it doesn’t depend on successive frames to determine the orientation. One of the applications could be for the implementation of yaw control of drone [2] in an indoor environment keeping camera on the feedback for the control.

REFERENCES

1. Dulio Furtado, Fulton T. Ray, A Rule Based 2-D Vision System to Determine Part Orientation, IFAC Proceedings Volumes, Volume 25, Issue 28, 1992, Pages 287-293.
2. N. Shijith and M. M. Dharmana, ”Sonar based terrain estimation & automatic landing of swarm quadrotors,” 2017 International Conference on Circuit ,Power and Computing Technologies (ICCPCT), Kollam, 2017, pp. 1-4.
3. A. Alexander and M. M. Dharmana, ”Object detection algorithm for segregating similar coloured objects and database formation,” 2017 International Conference on Circuit ,Power and Computing Technologies (ICCPCT), Kollam, 2017, pp. 1-5.
4. C. Tsai, C. Wong, T. Liu and A. Tsao, ”A novel image-based object orientation estimation algorithm for robotic manipulator applications,” 2012 International Symposium on Intelligent Signal Processing and Communications Systems, Taipei, 2012, pp. 280-284.
5. V. Sintunata and T. Aoki, ”Object orientation estimation for high speed 3D object retrieval system,” 2016 4th International Conference on Information and Communication Technology (ICoICT), Bandung, 2016, pp. 1-6.
6. C. Ks and H. Nicolas, ”Rough compressed domain camera pose estima- tion through object motion,” 2009 16th IEEE International Conference on Image Processing (ICIP), Cairo, 2009, pp. 3481-3484.
7. TaryudiandM.Wang,”3Dobjectposeestimationusingstereovisionfor object manipulation system,” 2017 International Conference on Applied System Innovation (ICASI), Sapporo, 2017, pp. 1532-1535.
8. J. Ku, A. D. Pon, S. Walsh and S. L. Waslander, ”Improving 3D Object Detection for Pedestrians with Virtual Multi-View Synthesis Orientation Estimation,” 2019 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Macau, China, 2019, pp. 3459-3466.